机器学习算法的广义分类大概有三种：监督式学习、无监督学习、强化学习。
监督学习由一个目标变量或结果变量（或因变量）组成。这些变量由已知的一系列预示变量（自变量）预测而来。利用这一系列变量，我们生成一个将输入值映射到期望输出值的函数。这个训练过程会一直持续，直到模型在训练数据上获得期望的精确度。监督式学习的例子有：回归、决策树、随机森林、K – 近邻算法、逻辑回归等。
无监督式学习没有任何目标变量或结果变量要预测或估计。这个算法用在不同的组内聚类分析。这种分析方式被广泛地用来细分客户，根据干预的方式分为不同的用户组。非监督式学习的例子有：关联算法和 K – 均值算法。
强化学习，这个算法训练机器进行决策。它的工作机制是机器被放在一个能让它通过反复试错来训练自己的环境中。机器从过去的经验中进行学习，并且尝试利用了解最透彻的知识作出精确的商业判断。 强化学习的例子有马尔可夫决策过程。

常见的十种机器学习算法：

1. 线性回归
2. 逻辑回归
3. 决策树算法
4. SVM支持向量机
5. 朴素贝叶斯
6. k近邻算法
7. k-means算法
8. 随机森林算法
9. 降维算法
10. Gradient Boosting 和 AdaBoost 算法

1、 线性回归
线性回归通常用于根据连续变量估计实际数值（房价，呼叫次数等），我们通过拟合最佳直线来建立自变量和因变量的关系，而这条最佳直线就叫做回归线，并且可以用

Y= a*X + b

线性等式来表示。
理解线性回归的最好办法是回顾一下童年。假设在不问对方体重的情况下，让一个五年级的孩子按体重从轻到重的顺序对班上的同学排序，你觉得这个孩子会怎么做？他（她）很可能会目测人们的身高和体型，综合这些可见的参数来排列他们。这是现实生活中使用线性回归的例子。实际上，这个孩子发现了身高和体型与体重有一定的关系，这个关系看起来很像上面的等式。
在上面的等式中，

• Y: 因变量
• X: 自变量
• a: 斜率
• b: 截距
  系数a和b可以通过最小二乘法求得；
  线性回归的两种主要类型是一元线性回归和多元线性回归。一元线性回归的特点是只有一个自变量。多元线性回归存在多个自变量。找最佳拟合直线的时候，你可以拟合到多项或者曲线回归。这些就被叫做多项或曲线回归。Python中sklearn中有这个算法，

from sklearn import linear_model

#Load Train and Test datasets
#Identify feature and response variable(s) and values must be numeric and numpy arrays
x_train=input_variables_values_training_datasets
y_train=target_variables_values_training_datasets
x_test=input_variables_values_test_datasets

# Create linear regression object
linear = linear_model.LinearRegression()

# Train the model using the training sets and check score
linear.fit(x_train, y_train)
linear.score(x_train, y_train)

#Equation coefficient and Intercept
print('Coefficient: n', linear.coef_)
print('Intercept: n', linear.intercept_)

#Predict Output
predicted= linear.predict(x_test)

2、逻辑回归
别被它的名字迷惑了！这是一个分类算法而不是一个回归算法。该算法可根据已知的一系列因变量估计离散数值（比方说二进制数值 0 或 1 ，是或否，真或假）。简单来说，它通过将数据拟合进一个逻辑函数来预估一个事件出现的概率。因此，它也被叫做逻辑回归。因为它预估的是概率，所以它的输出值大小在 0 和 1 之间（正如所预计的一样）。
假设你的朋友让你解开一个谜题。这只会有两个结果：你解开了或是你没有解开。想象你要解答很多道题来找出你所擅长的主题。这个研究的结果就会像是这样：假设题目是一道十年级的三角函数题，你有 70%的可能会解开这道题。然而，若题目是个五年级的历史题，你只有30%的可能性回答正确。这就是逻辑回归能提供给你的信息。

从数学上看，在结果中，几率的对数使用的是预测变量的线性组合模型。

from sklearn.linear_model import LogisticRegression
model = LogisticRegression()

model.fit(X, y)
model.score(X, y)

#Equation coefficient and Intercept
print('Coefficient: n', model.coef_)
print('Intercept: n', model.intercept_)

#Predict Output
predicted= model.predict(x_test)

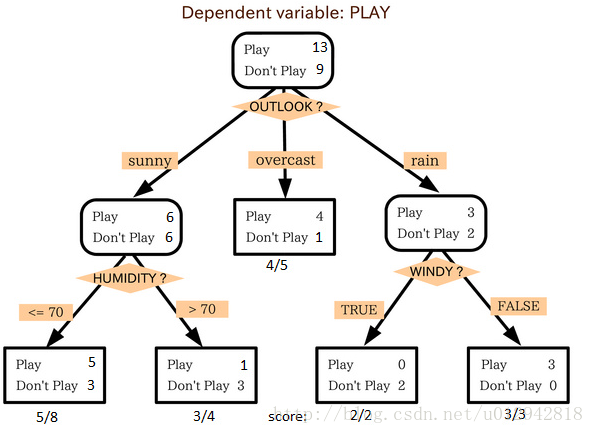
3、决策树
这个监督式学习算法通常被用于分类问题。令人惊奇的是，它同时适用于分类变量和连续因变量。在这个算法中，我们将总体分成两个或更多的同类群。这是根据最重要的属性或者自变量来分成尽可能不同的组别。

在上图中你可以看到，根据多种属性，人群被分成了不同的四个小组，来判断 “他们会不会去玩”。为了把总体分成不同组别，需要用到许多技术，比如说 Gini、Information Gain、Chi-square、entropy。

from sklearn import tree

#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create tree object 
model = tree.DecisionTreeClassifier(criterion='gini') # for classification, here you can change the algorithm as gini or entropy (information gain) by default it is gini  

# model = tree.DecisionTreeRegressor() for regression
# Train the model using the training sets and check score

model.fit(X, y)
model.score(X, y)

#Predict Output
predicted= model.predict(x_test)

4、支持向量机SVM
这是一种分类方法。在这个算法中，我们将每个数据在N维空间中用点标出（N是你所有的特征总数），每个特征的值是一个坐标的值。
支持向量机（Support Vector Machine，常简称为SVM）是一种监督式学习的方法，可广泛地应用于统计分类以及回归分析。支持向量机属于一般化线性分类器，这族分类器的特点是他们能够同时最小化经验误差与最大化几何边缘区，因此支持向量机也被称为最大边缘区分类器。
支持向量机将向量映射到一个更高维的空间里，在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面，分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大，分类器的总误差越小。
假设给定一些分属于两类的2维点，这些点可以通过直线分割， 我们要找到一条最优的分割线，如何来界定一个超平面是不是最优的呢?

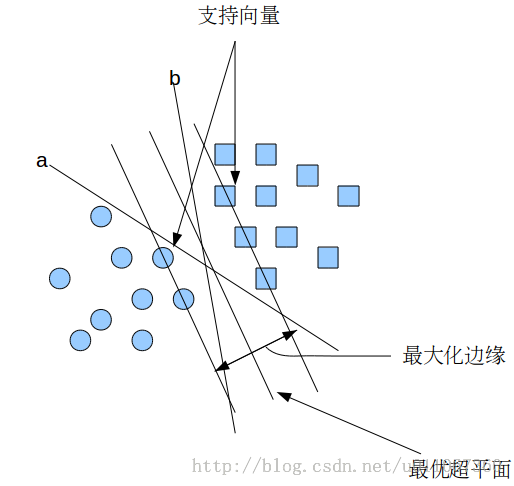
在上面的图中，a和b都可以作为分类超平面，但最优超平面只有一个，最优分类平面使间隔最大化。 那是不是某条直线比其他的更加合适呢? 我们可以凭直觉来定义一条评价直线好坏的标准:
距离样本太近的直线不是最优的，因为这样的直线对噪声敏感度高，泛化性较差。 因此我们的目标是找到一条直线（图中的最优超平面），离所有点的距离最远。 由此， SVM算法的实质是找出一个能够将某个值最大化的超平面，这个值就是超平面离所有训练样本的最小距离。这个最小距离用SVM术语来说叫做间隔(margin) 。
5、朴素贝叶斯
贝叶斯分类是一类算法的总称，这类算法均以贝叶斯定理为基础，故称为贝叶斯分类；
这个定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：
P(B|A)表示事件B已经发生的前提下，事件A发生的概率，称为事件B发生下事件A的条件概率，其基本求解公式为：
。
贝叶斯定理之所以有用，是因为在我们日常生活中经常遇到这种情况：我们可以很容易得出P(A|B)，但是P(B|A)则很难直接得出，，但是P(B|A)才是我们所关心的，贝叶斯定理就是为我们解决从P(A|B)获得P(B|A)的。
贝叶斯定理：。
朴素贝叶斯分类的原理和流程
朴素贝叶斯是一种十分简单的分类算法，叫他朴素贝叶斯是因为这种方法的思想“朴素”，思想基础是这样的：对于给出的待分类项，求解再此项出现的条件下各个类别出现的概率，哪个最大，就认为此代分类项属于哪个类别，通俗来讲，就好比这么个道理，你在街上看到一个和偶人，我问你猜这哥们哪里来的，你很可能会回答非洲。为什么呢？因为非洲人中黑人比率最高呀！当然人家也可能是美洲人或者亚洲人，但在没有其他可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。
1、设为一个待分类项，而每个a为x的一个特征属性。
2、有类别集合；
3、计算；
4、如果；
那么现在的关键是如何计算第三步中的条件概率，我们可以这样做：
1、找到一个一直分类的待分类集合，这个集合叫做训练样本集；
2、统计得到在各类别下各个特征属性的条件概率估计，即
；
3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：；
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：
；
根据上述分析，朴素贝叶斯分类的流程可以由下图表示（暂时不考虑验证）：

可以看到，整个朴素贝叶斯分类分为三个阶段：
第一阶段: 准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段: 分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。
第三阶段: 应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。