第一章    算法简介

1    二分查找

二分查找是一种算法，其输入是一个有序的元素列表。如果要查找的元素包含在列表中，二分查找返回其位置；否则返回null。

猜想1-100中的一个数字，7次内就能猜到。

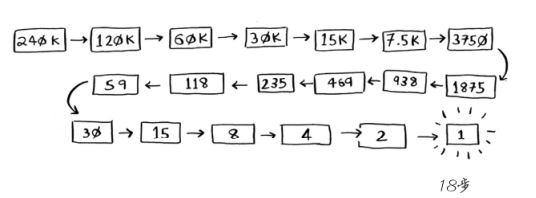
如果是在240000个单词的字典中找寻一个单词，只需要18步。

对于包含n个元素的列表，用二分查找最多需要logn步（这里log都是以2为底的），简单查找最多需要n步。

PS:仅当列表是有序的时候，二分查找才有效

python代码（这个好像只是简单查找呢）：

def binary_search(list, item):                #定义一个查找函数，接受参数列表和查找值
    low = 0                                   #low代表第一个索引
    high = len(list)-1                        #high代表最后一个索引
    while low <= high:                        
        mid = (low + high)                    #取中间索引值
        guess = list[mid]                     #中间索引对应列表中的值赋给猜想值
        if guess == item:                     #如果猜想值==查找值
            return mid
        if guess > item:                      #如果大于，那么就要要调整high的索引值，用mid-1代替，因为mid不是
            high = mid - 1                    
        else:                                 #小于则是low
            low = mid + 1
    return None
my_list = [1, 3, 5, 7, 9]
print(binary_search(my_list, 3))
print(binary_search(my_list, -1))

练习：

1.1 假设有一个包含128个名字的有序列表，你要使用二分查找在其中查找一个名字，请

问最多需要几步才能找到？

log128 = 7 ， 最多需要七步找到。

1.2 上面列表的长度翻倍后，最多需要几步？

log256 = 8 ， 最多需要八步找到。

2    运行时间

最多需要猜测的次数与列表长度相同，这被称为线性时间（linear time）——O（n）

二分查找的运行时间为对数时间（或log时间）——O（logn）

3    大O表示法

大O表示法让你能够比较操作数，它指出了算法运行时间的增速。

大O表示法是这样的：

PS：大O表示法说的是最糟糕的情况。

4     一些常见的大O运行时间（又快到慢）

 O(log n)，也叫对数时间，这样的算法包括二分查找。
 O(n)，也叫线性时间，这样的算法包括简单查找。
 O(n  * log n)，这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
 O(n 2 )，这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。

 O(n!)，这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。

面按从快到慢的顺序列出了使用这些算法绘制网格所需的时间：

PS：算法的速度指的并非时间，而是操作数的增速。

谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。

算法的运行时间用大O表示法表示。

O(log n)比O(n)快，当需要搜索的元素越多时，前者比后者快得越多。

练习：使用大O表示法给出下述各种情形的运行时间

1.3 在电话簿中根据名字查找电话号码。

O(logn)

1.4 在电话簿中根据电话号码找人。（提示：你必须查找整个电话簿。）

O(n)

1.5 阅读电话簿中每个人的电话号码。

O(n)

1.6 阅读电话簿中姓名以A打头的人的电话号码。这个问题比较棘手，它涉及第4章的概念。答案可能让你感到惊讶！

O(n)，大O表示法不考虑乘以、除以、加上或减去的数字