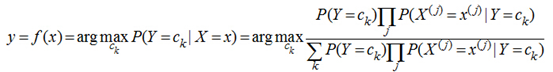1 概述
贝叶斯分类算法是一大类分类算法的总称。贝叶斯分类算法以样本可能属于某类的概率来作为分类依据。朴素贝叶斯(Naive Bayes)分类算法是贝叶斯分类算法中最简单的一种。
注:朴素的意思是条件概率独立性
2 算法思想
朴素贝叶斯的思想是这样的:如果一个事物在一些属性条件发生的情况下,事物属于A的概率>属于B的概率,则判定事物属于A。
通俗来说,你在街上看到一个黑人,让你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
3 示例
3.1 比如在某条大街上,有100人,其中有50个美国人,50个非洲人,看到一个讲英语的黑人,那么我们是怎么去判断他来自哪里?
提取特征:
肤色:黑,语言:英语
先验知识:
P(黑色|非洲人) = 0.8
P(讲英语|非洲人)=0.1
P(黑色|美国人)= 0.2
P(讲英语|美国人)=0.9
要判断的概率是:
P(非洲人|(讲英语,黑色) )
P(美国人|(讲英语,黑色) )
思考过程:

P(非洲人|(讲英语,黑色) ) 的 分子= 0.1 * 0.8 *0.5 =0.04
P(美国人|(讲英语,黑色) ) 的 分子= 0.9 *0.2 * 0.5 = 0.09
从而比较这两个概率的大小就等价于比较这两个分子的值,可以得出结论,此人应该是:美国人。
其蕴含的数学原理如下:
p(A|xy)=p(Axy)/p(xy)=p(Axy)/p(x)p(y)=p(A)/p(x)*p(A)/p(y)* p(xy)/p(xy)=p(A|x)p(A|y)
|
朴素贝叶斯分类器 讲了上面的小故事,我们来朴素贝叶斯分类器的表示形式:
当特征为为x时,计算所有类别的条件概率,选取条件概率最大的类别作为待分类的类别。由于上公式的分母对每个类别都是一样的,因此计算时可以不考虑分母,即
朴素贝叶斯的朴素体现在其对各个条件的独立性假设上,加上独立假设后,大大减少了参数假设空间。 |
4 算法要点
4.1 算法步骤
1. 分解各类先验样本数据中的特征;
2. 计算各类数据中,各特征的条件概率;(比如:特征1出现的情况下,属于A类的概率p(A|特征1),属于B类的概率p(B|特征1),属于C类的概率p(C|特征1)......)
3. 分解待分类数据中的特征(特征1、特征2、特征3、特征4......)
4. 计算各特征的各条件概率的乘积,如下所示:
判断为A类的概率:p(A|特征1) * p(A|特征2) * p(A|特征3) * p(A|特征4)......
判断为B类的概率:p(B|特征1) * p(B|特征2) * p(B|特征3) * p(B|特征4)......
判断为C类的概率:p(C|特征1) * p(C|特征2) * p(C|特征3) * p(C|特征4)......
......
5. 结果中的最大值就是该样本所属的类别
4.2 算法应用举例
大众点评、淘宝等电商上都会有大量的用户评论,比如:
|
1、衣服质量太差了!!!!颜色根本不纯!!! 2、我有一有种上当受骗的感觉!!!! 3、质量太差,衣服拿到手感觉像旧货!!! 4、上身漂亮,合身,很帅,给卖家点赞 5、穿上衣服帅呆了,给点一万个赞 6、我在他家买了三件衣服!!!!质量都很差! |
0 0 0 1 1 0 |
其中1/2/3/6是差评,4/5是好评
现在需要使用朴素贝叶斯分类算法来自动分类其他的评论,比如:
|
a、这么差的衣服以后再也不买了 b、帅,有逼格 …… |
4.3 算法应用流程
1. 分解出先验数据中的各特征
(即分词,比如“衣服”,“质量太差”,“差”,“不纯”,“帅”,“漂亮”,“赞” ......)
2. 计算各类别(好评、差评)中,各特征的条件概率
(比如 p(“衣服” | 差评)、p(“衣服” | 好评)、p(“差”|好评)、p(“差”| 差评) ......)
3. 计算类别概率
p(好评|(c1,c2,c5,c8))的分子=p(c1|好评) * p(c2|好评) * p(c3|好评) *......p(好评)
p(差评|(c1,c2,c5,c8))的分子=p(c1|差评) * p(c2|差评) * p(c3|差评) *......p(差评)

4. 显然p(差评)的结果值更大,因此a被判别为"差评"
5 朴素贝叶斯分类算法案例
5.1 需求
利用大量邮件先验数据,使用朴素贝叶斯分类算法来自动识别垃圾邮件
5.2 python实现
请参考《机器学习实战》中的 垃圾邮件 过滤部份