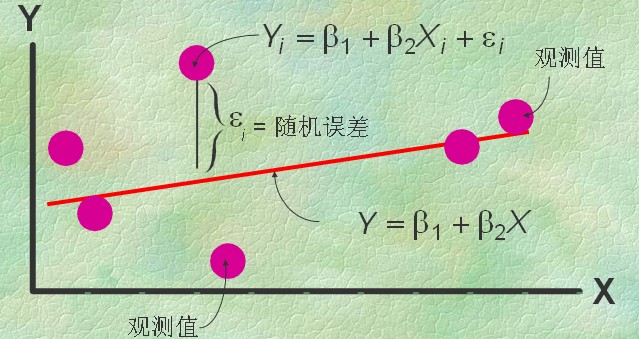
一元线性回归
1. 预测房价房价是一个很火的话题,现在我们拿到一组数据,是房子的大小(平方英尺)和房价(美元)之间的对应关系,如下(csv数据文件):
No,square_feet,price
1,150,6450
2,200,7400
3,250,8450
4,300,9460
5,350,11400
6,400,15470
7,600,18455
问410平方的房子是多少钱? 一元线性回归就是解决上面例子用的。
我现在有这么一张图,横坐标代表房子的面积,纵坐标代表房价。然后呢,一元线性回归就是要找一条直线,并且让这条直线尽可能地拟合图中的数据点。那既然是找直线,那肯定是要有一个评判的标准,来评判哪条直线才是最好的。那咋评判呢?其实只要算一下实际房价和我找出的直线根据房子大小预测出来的房价之间的差距就行了。说白了就是算两点的距离。当我们把所有实际房价和预测出来的房价的差距(距离)算出来然后做个加和,我们就能量化出现在我们预测的房价和实际房价之间的误差。例如下图中我画了很多条小数线,每一条小数线就是实际房价和预测房价的差距(距离)
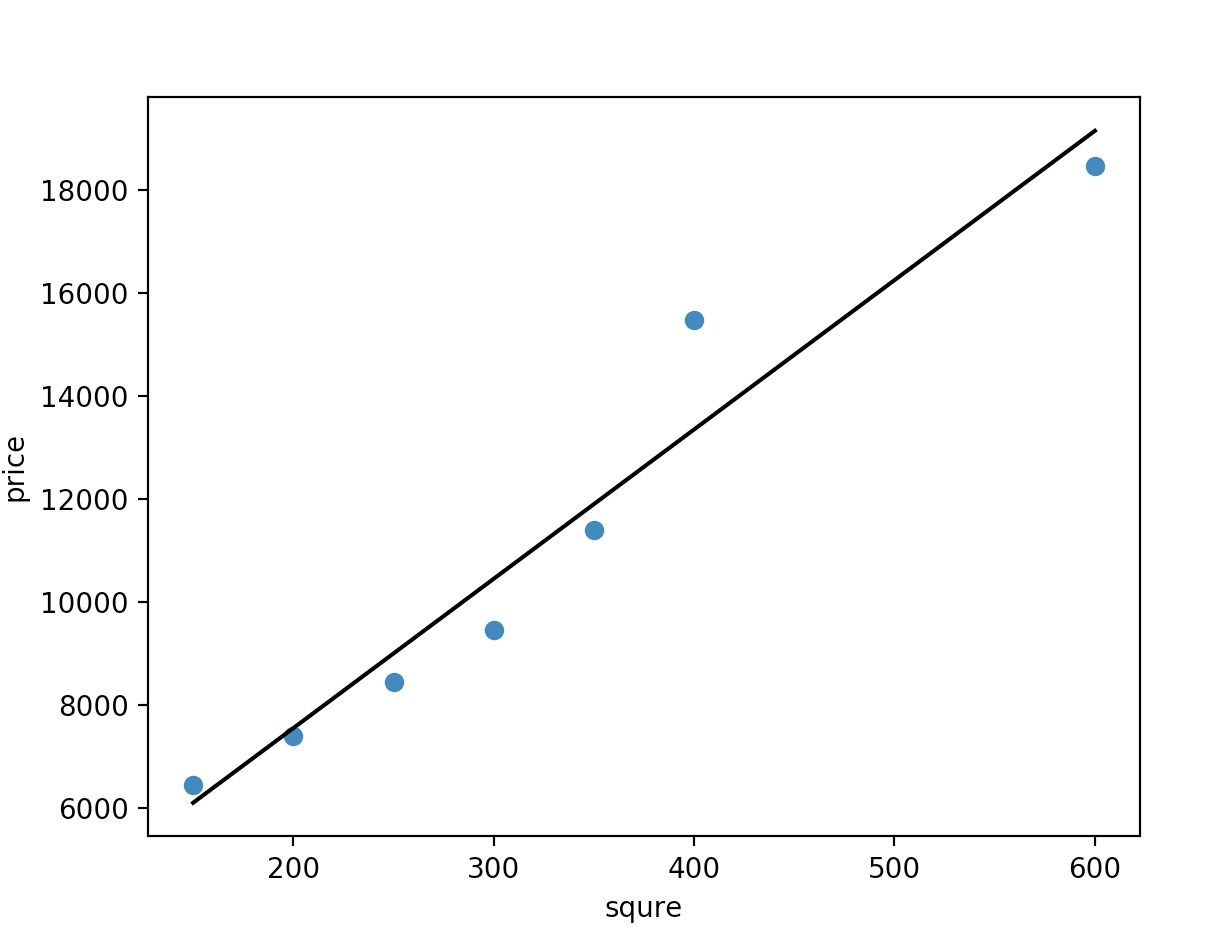
然后把每条小竖线的长度加起来就等于我们现在通过这条直线预测出的房价与实际房价之间的差距。那每条小竖线的长度的加和怎么算?其实就是欧式距离加和,公式如下。(其中y(i)表示的是实际房价,ŷ(i)表示的是预测房价)
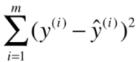
这个欧氏距离加和其实就是用来量化预测结果和真实结果的误差的一个函数。在ML中称它为损失函数(说白了就是计算误差的函数)。那有了这个函数,我们就相当于有了一个评判标准,当这个函数的值越小,就越说明我们找到的这条直线越能拟合我们的房价数据。所以说啊,线性回归无非就是通过这个损失函数做为评判标准来找出一条直线。
2. 思路总结
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2),…,(Xn,Yn)。对于平面中的这n个点,可以使用无数条直线来拟合。选择最佳拟合直线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)
也就是求 y=b0+b1x 的最佳参数,其中需要一个标准来对结果进行衡量,为此我们需要定量化一个目标函数式,使得计算机可以在求解过程中不断地优化。
针对任何模型求解问题,都是最终都是可以得到一组预测值y^ ,对比已有的真实值 y ,数据行数为 n ,可以将损失函数定义如下:
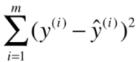
即预测值与真实值之间的平均的平方距离, 求解方式有两种:
1)最小二乘法(least square method)
求解 b1 和 b0 是使损失函数最小化的过程, 得到如下
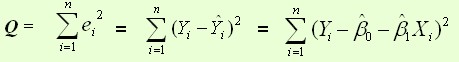
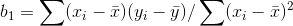

式中,x{i}为对于第i次观测,自变量的值,y{i}为对于第i次观测,应变量的观测值;x-为自变量的样本平均值,ȳ为应变量的样本平均值,n为总观测次数
2)梯度下降(gradient descent)
忽略,暂时不讲
python代码
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def fitSLR(x, y):
#训练简单线性模型
n = len(x) # 获取数据集长度
dinominator = 0 # 分母
numerator = 0 # 分子
for i in range(0, n):
numerator += (x[i] - np.mean(x))*(y[i] - np.mean(y))
dinominator += (x[i] - np.mean(x))**2
b1 = numerator/float(dinominator) # 回归线斜率
b0 = np.mean(y)-b1*np.mean(x) # 回归线截距
b1 = round(b1)
b0 = round(b0)
return b0, b1
def predict(x, b0, b1):
#根据学习算法做预测
return b0 + x*b1
if __name__ == "__main__":
x = [150,200,250,300,350,400,600]
y = [6450,7400,8450,9460,11400,15470,18455]
b0, b1 = fitSLR(x, y)
print("intercept:", b0, " slope:", b1)
testData = 410
result = predict(testData, b0, b1)
print(result)
y_perd = b0 + b1*np.array(x)
plt.scatter(x, y) #散点图
plt.plot(x, y_perd, color=black)
plt.xlabel("squre")
plt.ylabel("price")
plt.show()
相关理论知识
一元线性回归是描述两个变量之间相关关系的最简单的回归模型。自变量与因变量间的线性关系的数学结构通常用式(1)的形式:
y = β1 + β2x + ε (1)
式(1)称为变量y对x的一元线性回归理论模型。一般称y为因变量,x为自变量,β1和β2是未知参数,称β1为回归常数,β2为回归系数。ε表示误差项,它是一个随机变量。