前面已经讲过一元线性回归，参考机器学习--- 一元线性回归

1. 理论

现在讲讲多元线性回归， 我们之前开发的线性回归仅能处理单一的特征x，也就是房子的面积，而且我们仅仅依赖它来预测房子的价格。我们如果真的去预测一套房子的价格的话，单单依靠房子的面积肯定是不够的。因为影响房价的因素肯定不仅仅是面积。比如，有几个卧室呀，有几个卫生间呀，房龄多久了呀等等。

即:

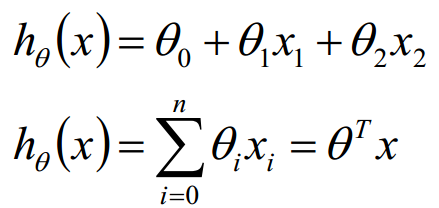
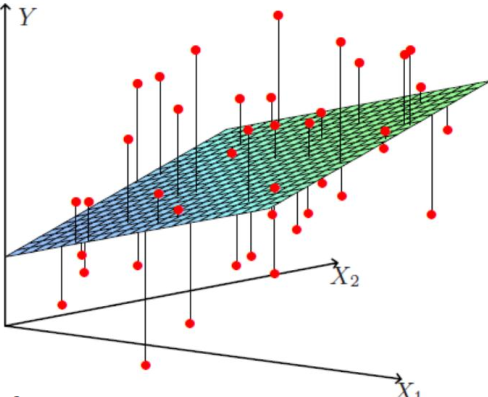
也就是以下方程

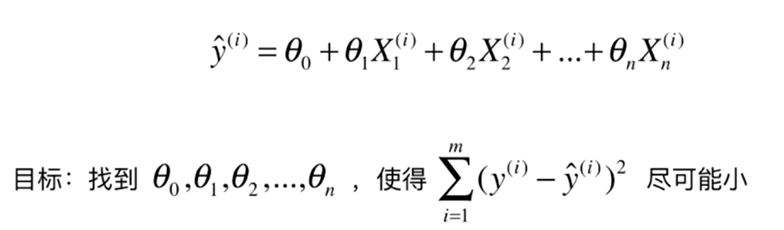
经过转换，等到以下 目标函数（损失函数）为

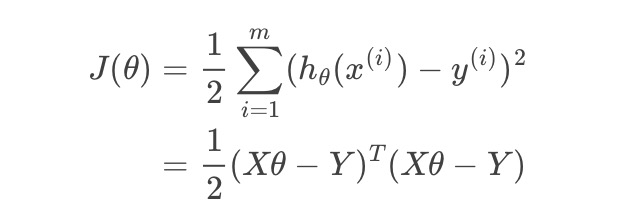
经过一系列运算，得到的结果为 最终求的解析解为：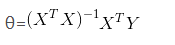

2. Python代码实现

以如下数据为例，对运输里程、运输次数与运输总时间的关系，建立多元线性回归模型：

2.1 python 原生实现

# -*- coding: UTF-8 -*-

import numpy as np

class LinearRegression:
  def __init__(self):
    初始化模型
    self.coef_ = None
    self.interception_ = None
    self._theta = None

  def fit_normal(self,X_train,y_train):
    根据训练数据集X_train,y_train训练模型
    assert X_train.shape[0] == y_train.shape[0],the number of X_train must equal to the number of y_train
    X_b = np.hstack([np.ones((len(X_train),1)),X_train])
    
    self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
    self.interception_ = self._theta[0]
    self.coef_ = self._theta[1:]
    return self
    
  def predict(self,X_predict):
    assert self._theta is not None,must fit before predict
    assert X_predict.shape[1] == len(self.coef_),the feature number of X_predict must equal to X_train 

    X_b = np.hstack([np.ones((len(X_predict),1)),X_predict])
    return X_b.dot(self._theta)

  def score(self,X_test,y_test):
    根据测试数据集确定当前模型的准确度
    #todo
    y_predict = self.predict(X_test)    
  

#使用
x = np.array([[100,4,9.3],[50,3,4.8],[100,4,8.9],
              [100,2,6.5],[50,2,4.2],[80,2,6.2],
              [75,3,7.4],[65,4,6],[90,3,7.6],[90,2,6.1]])
X_train = x[:,:-1]
y_train = x[:,-1]
#print(X_train)
#print(y_train)

reg = LinearRegression()
reg.fit_normal(X_train,y_train)
#print(reg.interception_)
#print(reg.coef_)
# 预测
X_test = np.array([[102,6],[100,4]])
y_predict = reg.predict(X_test)
print(y_predict)  #[10.90757981  8.93845988]

2.2 sklearn实现

import numpy as np
from sklearn import datasets,linear_model

# 定义训练数据
x = np.array([[100,4,9.3],[50,3,4.8],[100,4,8.9],
              [100,2,6.5],[50,2,4.2],[80,2,6.2],
              [75,3,7.4],[65,4,6],[90,3,7.6],[90,2,6.1]])
print(x)
X = x[:,:-1]
Y = x[:,-1]
print(X,Y)

# 训练数据
regr = linear_model.LinearRegression()
regr.fit(X,Y)
print(coefficients(b1,b2...):,regr.coef_)
print(intercept(b0):,regr.intercept_)

# 预测
x_test = np.array([[102,6],[100,4]])
y_test = regr.predict(x_test)
#评分
print(regr.score(x_test,y_test))
#结果
print(y_test)  # [10.90757981  8.93845988]

以上2种实现方式的结果是一致的